Red blood cells are the major cellular component of blood. Mature red blood cells are biconcave discs that lack nucleus and most cell organelles such as lysomes, endoplasmic reticulum and mitochondria. However, variable abnormal erythrocyte morphology is found in various pathological conditions:
- Anisocytosis: Variation in size
- Poikilocytosis: Variation in shape
- Variation in color
- Presence of inclusion bodies
Anisocytosis : Variation in size
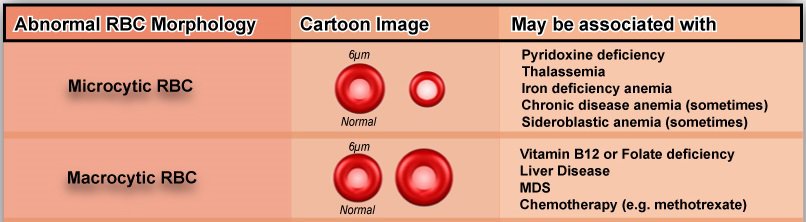
Variation of size of RBC is called anisocytosis. The normal size of RBC is 7.5+/-0.2 micrometer in diameter. Nucleus of small lymphocyte is useful guide to the size of RBC. Anisocytosis is divided into Macrocytosis and Microcytosis.
- Microcytosis: RBCs smaller than the normal size are considered as microcytes. Microcytosis is seen in : Iron deficiency anemia, thalassemia, lead poisoning, sideroblastic anemia and anemia of chronic disorders.
- Macrocytosis: RBCs larger than the normal size are considered as macrocytes. Macrocytosis is seen in : Liver diseases, hypothyroidism, megaloblastic anemia, chemotherapy, post splenectomy and some other causes of elevated erythropoiesis.
READ ABOUT: Complete blood cell count tests
Variaton in color
RBCs that appear disc shaped and having an area of central pallor that occupies approximately one-third of the cell’s diameter (containing normal amount of hemoglobin) are considered as normochromic RBCs.
- Hypochromic : RBCs that have an area of pallor that is larger than the normal are called hypochromic. This variation is seen in : Iron deficiency anemia, anemia of chronic diseases, thalassemia, some hemoglobinopathies, sideroblastic anemia and any of the conditions leading to microcytosis.
Poikilocytosis : Variation in shape
Variation in the shape of RBC is called poikilocytosis. RBCs exist as biconcave discs in large blood vessels but their shape changes to parachute like confirmation in capillaries. Following are some abnormal RBC shapes :
- Spherocytes: RBCs lacks the biconcave shape and becomes more spherical, no central pallor is present with increased hemoglobin content.
- Ovalocytes: Oval shaped RBCs.
- Elliptocytes: The RBCs are ovaal or elliptical in shape, long axis is twice the short axis.
- Target cells: Red cells have an area of increased staining which appears in the area of central pallor.
- Teardrop cells: RBCs having the shape like teardrop or pear. These are usually microcytic and often hypochromic.
- Schistocytes: These are helmet or triangular shaped, fragmented or greatly distorted RBCs smaller than normal size.
- Acanthocytes: RBCs with irregularly spaced projections. Projections vary in width but usually contain a rounded end.
- Stomatocytes: Red cells with a central linear slit or stoma. Seen as mouth shaped form in peripheral smear.
- Keratocytes: These are half-moon shaped cells with two or more spicules.
- Burr cells: Red cells with uniformly spaced pointed projections on their surface.
- Sickle cells: These are sickle-shaped Red Blood Cells.
- Red cell agglutinate: These are irregular clumps of RBCs.
- Rouleaux Formation: Stacks of RBCs resembling a stack of coins.
Spherocytes are found in : hereditary spherocytosis, hemolytic anemia and post transfusion reaction.
Ovalocytes are found in : Thalassemia major, hereditary ovalocytosis, sickle cell anemia.
Elliptocytes are found in : hereditary elliptocytosis, megaloblastic anemia, IDA, thalassemia, myelofibrosis.
Target cells are found in : obstructive liver disease, severe IDA, thalassemia, Hemoglobinopathies, post splenectomy.
Teardrop cells are found in : myelofibrosis, megaloblastic anemia, IDA, thalassemia.
Schistocytes are seen in : Thalassemia, microangiopathic hemolytic anemia, mechanical hemolytic anemia, uremia, artificial heart valves.
Acanthocytes are found in : liver diseses, post splenectomy, anorexia nervosa and starvation, alcoholism, vitamin C deficiency.
Stomatocytes are found in : excess alcoholism, alcoholic liver disease, heref=ditary stomatocytosis.
Keratocytosis is seen in G6PD deficiency, pulmonary embolism, disseminated intravascular coagulation.
Burr cells are found in hemolytic anemia, uremia, megaloblastic anemia.
Sickle cells are seen in Hb-S disease/ sickle cell anemia.
These are found in cold agglutinations, warm autoimmune hemolysis.
These are found in hyperglobulinemia, hyperfibrinogenaemia.
Presence of Inclusion Bodies
Red blood cells have different morphological variations depending upon following type of inclusion bodies :
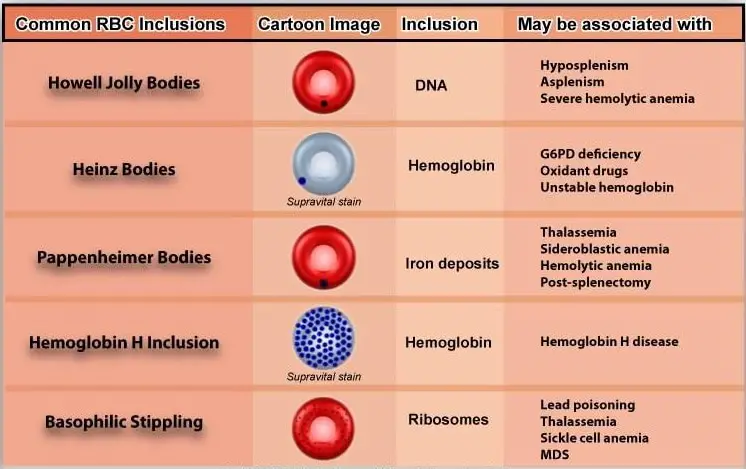
- Howell-Jolly bodies: Small round cytoplasmic red cell inclusion with same staining characteristics as nuclei. These are fragments of DNA.
- Heinz bodies: These represent denatured hemoglobin (methemoglobin) within a cell. With a supravital stain like crystal violet, Heinz bodies appear as round blue precipitates.
- Pappenheimer bodies: These represent iron deposits which as dense blue, irregular granules in wright stain.
- Basophilic stippling: These are considerable amount of small basophilic inclusions in red cells which represent precipitated RNA.
- Cabbot’s ring: Reddish, purple, thread-like rings in RBCs of severe anemias.
- Parasites of red cells: Protozoan parasites like one of the four species of the malarial parasite may be seen in case of malarial infection.
Usually seen in Post splenectomy, MBA, hemolytic anemia.
Seen in G6PD Deficiency, splenectomy.
Pappenheimer bodies are found in RBCs with hemolytic anemia, splenectomy, sideroblastic anemia, thalassemia.
Seen in : thalassemia, MBA, hemolytic anemia, liver damage, heavy metal poisoning.
These are the remnants of nuclear membrane.





No comments:
Post a Comment
Due to the high number of spammy comments we have decided to initiate comment moderation so that we can maintain our quality standards and make good environment for our visitors. Please leave your comment